Bayes theory is like playing golf, without knowing where the hole is on the green. Imagine someone took the flag out of the hole on an elevated green. You are in the fairway and have to make a shot 20 feet up, and you want to leave your ball within inches of the hole. Normally there would be a flag in the hole, so you don’t have to walk all the way up to the green and search for the hole, you can just see where the flag is.
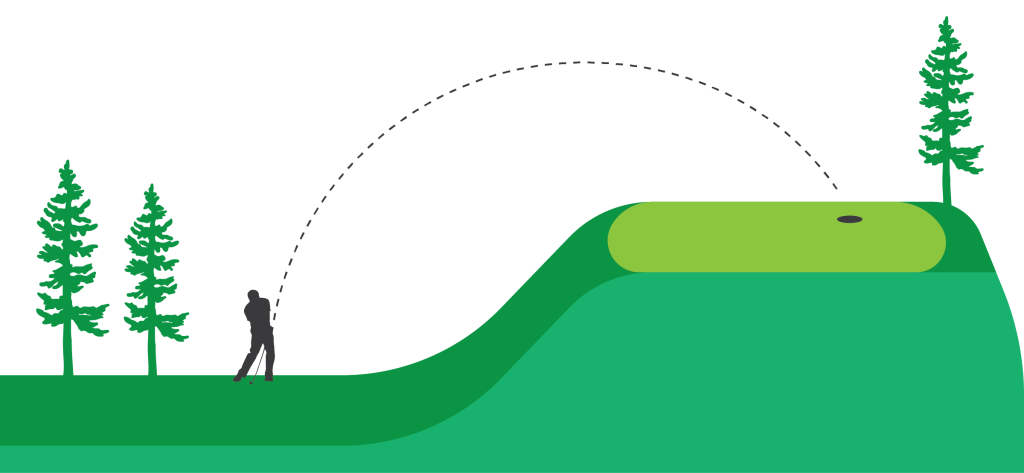
Now imagine there is a board next to your ball, and every person who hits throughout the day, comes back and writes information on the board about where their ball landed. As you can see some people were very descriptive and some weren’t

You can see, the first golfer was just happy to hit the green, especially since he had no idea where the cup was. But as the day goes on and more golfers comeback and report how they did, you can get a good idea of where the cup is and where you should aim.
Now compare this to inspection, different inspections have different effectiveness. Line number one would be considered an ineffective inspection because it doesn’t tell you where he landed his ball, or if there is even a hole on this green! At least the second guy was able to confirm that there is actually a hole, since he landed right in it. Line three isn’t bad, but still doesn’t tell you much, you know the hole is a long ways away from the front of the green, so near the back. The fourth golfer, gave you lots of information but it’s only about the depth of the hole, not how far left or right you should aim. Line 5 is another bad inspection. Line six we finally get information about aiming left or right, but if I want to get my ball inches from the hole, I need a little more information, like was he 3 feet short of the hole? Maybe he was 3 feet too far to the left of the hole. But, by using the information from golfer #4 and golfer #6 we have a really good idea of an area to hit to. Finally, golfer #7 was able to use all of the information on the board, lines 1-6, and was able to put the ball right next to the pin. Then he came back and described exactly where to aim and how far the ball went.
This example shows how constantly updating your knowledge, based on previous information can allow your future probability to increase. It also shows that not all information sets are equal. Some data gives you more useful information while other data provides essentially no information at all.
